Научное объяснение радуги впервые дал Рене Декарт в 1637 г. Декарт объяснил радугу на основании законов преломления и отражения солнечного света в каплях выпадающего дождя. В то время еще не была открыта дисперсия — разложение белого света в спектр при преломлении. Поэтому радуга Декарта была белой.
Спустя 30 лет Исаак Ньютон, открывший дисперсию белого света при преломлении, дополнил теорию Декарта, объяснив, как преломляются цветные лучи в каплях дождя. По образному выражению американского ученого А. Фразера, сделавшего ряд интересных исследований радуги уже в наше время, „Декарт повесил радугу в нужном месте на небосводе, а Ньютон расцветил ее всеми красками спектра".
Несмотря на то что теория радуги Декарта — Ньютона создана более 300 лет назад, она правильно объясняет основные особенности радуги: положение главных дуг, их угловые размеры, расположение цветов в радугах различных порядков.
Для объяснения радуги мы пока и ограничимся теорией Декарта — Ньютона, которая подкупает своей удивительной наглядностью и простотой.
Лучи радуги
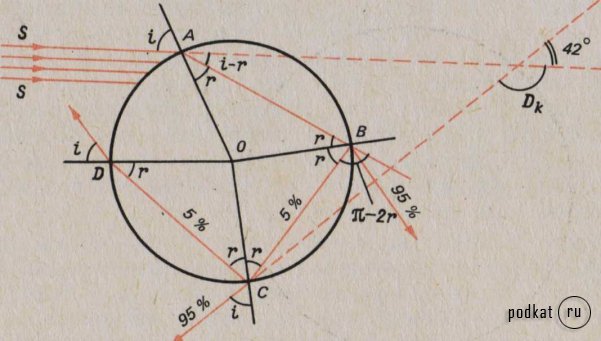
Итак, пусть параллельный пучок солнечных лучей падает на каплю (рис. 5.1). Ввиду того, что поверхность капли кривая, у разных лучей будут разные углы падения. Они изменяются от 0 до 90°. Проследим путь луча, упавшего в точку А, его угол падения обозначим i. Преломившись под углом преломления г, луч входит в каплю и доходит до точки В. Часть энергии луча, преломившись, выходит из капли, часть, испытав внутреннее отражение в точке В, идет внутри капли до точки С. Здесь снова часть энергии луча, преломившись, выходит из капли, а некоторая часть, испытав второе внутреннее отражение, доходит до точки D и т. д. В принципе луч может испытывать любое число(k)внутренних отражений, а преломлений у каждого луча два — при входе и при выходе из капли.
<!--ThumbBegin-->
<!--ThumbEnd-->
<!--ThumbEnd-->Рис. 5.1. Ход светового луча в капле при образовании первой и второй радуг.
Обозначим Dkугол отклонения любого луча после прохождения им капли. Тогда из рис. 5.1 очевидно, что
Dk =2(i -r) +k(Пи -2r), (5.1)
здесь k — число внутренних отражений луча.
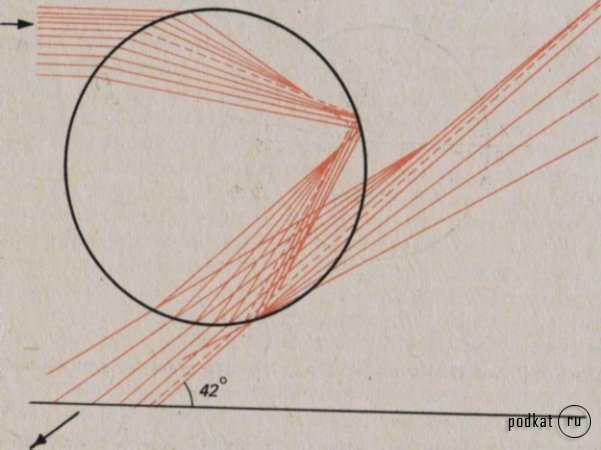
Параллельный пучок лучей, падающий на каплю, по выходе из капли оказывается сильно расходящимся (рис. 5.2). Концентрация лучей, а значит, и их интенсивность тем больше, чем ближе они лежат к лучу, испытавшему минимальное отклонение. Путь минимально отклоненного луча обозначен на рисунке пунктиром. Только минимально отклоненный луч и самые близкие к нему лучи обладают достаточной интенсивностью, чтобы образовать радугу. Поэтому этот луч и называют лучом радуги.
Минимальное отклонение луча, испытавшего одно внутреннее отражение (k = 1), по теории Декарта равно:
D1 = пи + 2(i — 2r). (5.2)
Каждый белый луч, преломляясь в капле, разлагается в спектр, и из капли выходит пучок расходящихся цветных лучей. Поскольку у красных лучей показатель преломления меньше, чем у других цветных лучей, то они и будут испытывать минимальное отклонение по сравнению с остальными. Минимальные отклонения крайних цветных лучей видимого спектра красных и фиолетовых оказываются следующими: D1k = 137°30/ и D1ф = = 139°20'. Остальные цветные лучи займут промежуточные между ними положения.
Солнечные лучи, прошедшие через каплю с одним внутренним отражением, оказываются исходящими от точек неба, расположенных ближе к антисолярной точке, чем к Солнцу. Поэтому, чтобы увидеть эти лучи, надо встать спиной к Солнцу. Расстояния их от антисолярной точки будут равны соответственно: 180° — 137°30' = 42°30' для красных и 180° — 139°20' = = 40°40' для фиолетовых.
<!--ThumbBegin-->
<!--ThumbEnd-->
<!--ThumbEnd-->Рис. 5.2. Преломление пучка световых лучей в капле.
Почему радуга круглая? Дело в том, что более или менее сферическая капля, освещенная параллельным пучком лучей солнечного света, может образовать радугу только в виде круга. Поясним это.
Описанный путь в капле с минимальным отклонением по выходе из нее проделывает не только тот луч, за которым мы следили, но также и многие другие лучи, упавшие на каплю под таким же углом. Все эти лучи и образуют радугу, поэтому их называют лучами радуги.
Сколько же лучей радуги в пучке света, падающего на каплю? Их много, по существу, они образуют целый цилиндр. Геометрическое место точек их падения на каплю это целая окружность.
В результате прохождения через каплю и преломления в ней цилиндр белых лучей преобразуется в серию цветных воронок, вставленных одна в другую, с центром в антисолярной точке, с открытыми раструбами, обращенными к наблюдателю. Наружная воронка красная, в нее вставлена оранжевая, желтая, далее идет зеленая и т. д., кончая внутренней фиолетовой.
Таким образом, каждая отдельная капля образует целую радугу! Радуга — „как Солнце в малой капле вод". Так образно и предельно лаконично выразил суть радуги Г. Р. Державин.
Конечно, радуга от одной капли слабая, и в природе ее невозможно увидеть отдельно, так как капель в завесе дождя много. В лаборатории же удавалось наблюдать не одну, а несколько радуг, образованных преломлением света в одной подвешенной капельке воды или масла при освещении ее лучом лазера.
Радуга, которую мы видим на небосводе, мозаична — она образована мириадами капель. Каждая капля создает серию вложенных одна в другую цветных воронок (или конусов). Но от отдельной капли в радугу попадает только один цветной луч. Глаз наблюдателя является общей точкой, в которой пересекаются цветные лучи от множества капель. Например, все красные лучи, вышедшие из различных капель, но под одним и тем же углом и попавшие в глаз наблюдателю, образуют красную дугу радуги, также и все оранжевые и другие цветные лучи. Поэтому радуга круглая. Два человека, стоящие рядом, видят каждый свою радугу. Если вы идете по дороге и смотрите на радугу, она перемещается вместе с вами, будучи в каждый момент образована преломлением солнечных лучей в новых и новых каплях. Далее, капли дождя падают. Место упавшей капли занимает другая и успевает послать свои цветные лучи в радугу, за ней следующая и т. д. Пока идет дождь, мы видим радугу.
ВОТ ТАК!!,а теперь фото-
<!--ThumbBegin-->
<!--ThumbEnd-->
<!--ThumbEnd--><!--ThumbBegin-->
<!--ThumbEnd-->
<!--ThumbEnd--><!--ThumbBegin-->
<!--ThumbEnd-->
<!--ThumbEnd--><!--ThumbBegin-->
<!--ThumbEnd-->
<!--ThumbEnd--><!--ThumbBegin-->
<!--ThumbEnd-->
<!--ThumbEnd-->
<!--ThumbBegin-->
<!--ThumbEnd-->
<!--ThumbEnd--><!--ThumbBegin-->
<!--ThumbEnd-->
<!--ThumbEnd--><!--ThumbBegin-->
<!--ThumbEnd-->
<!--ThumbEnd-->
<!--ThumbBegin-->
<!--ThumbEnd-->
<!--ThumbEnd--><!--ThumbBegin-->
<!--ThumbEnd-->
<!--ThumbEnd--><!--ThumbBegin-->
<!--ThumbEnd-->
<!--ThumbEnd--><!--ThumbBegin-->
<!--ThumbEnd-->
<!--ThumbEnd-->
